Aritméticas
y geométricas
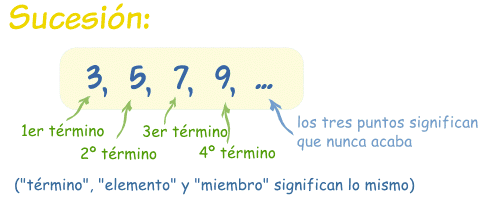
Toda secuencia ordenada de números reales recibe el nombre de sucesión.
Dentro del grupo de sucesiones existen dos particularmente interesantes por el
principio de regularidad que permite sistematizar la definición de sus
propiedades: las progresiones aritméticas y geométricas.

Progresiones aritméticas
Una progresión aritmética es una clase de sucesión de números reales en la que cada
término se obtiene sumando al anterior una cantidad fija predeterminada
denominada diferencia. Llamando d a esta diferencia, el término general de la progresión an , que
ocupa el número de orden n en la misma, se puede determinar a partir del valor
del primero de los términos, a1.
- an=a1+(n-1)d
Suma de los términos de una
progresión aritmética
Para determinar la suma de un número finito de términos de una
progresión aritmética, denotada por a1, a2, a3, ..., an-2, an-1, an, basta con considerar el principio de que los pares
de términos a1 y an, a2 y an-1, a3 y an-2, etcétera, son equidistantes,
de manera que todos estos pares suman una misma cantidad.
Generalizando esta consideración, se tiene que la suma de
todos los términos de una progresión aritmética es igual a:
- Sn= n/2 (a1+an)
Interpolación de términos en una progresión aritmética
Entre cada dos términos a y b de
una progresión aritmética es posible interpolar otros m términos, llamados medios diferenciales,
de manera que todos ellos integren una nueva progresión aritmética (con m + 2
términos) donde a y b sean los extremos.
La diferencia de esta progresión se determinará con arreglo
a la siguiente fórmula:
- Sn=n/2 {2a1+(n-1)d}
Progresiones geométricas
Otra forma común de sucesión es la
constituida por las llamadas progresiones geométricas. Estas progresiones se
definen como aquellas en las que cada término se obtiene multiplicando el
anterior por un valor fijo predefinido que se conoce comorazón.
El término general an de
una progresión geométrica puede escribirse como:
an = a1 × rn-1
- Sn=s1 (1-rn)/1-r
- Sn= a1-r.an/1-r
CRISTIAN RODRÍGUEZ MILLÁN
No comments:
Post a Comment